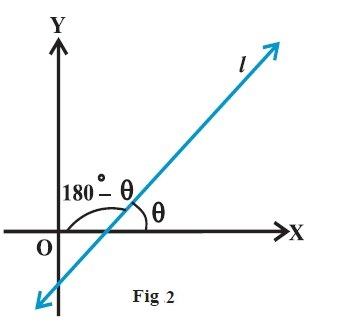
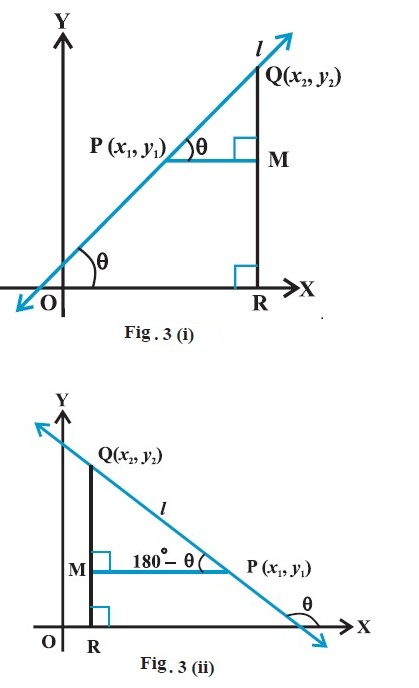
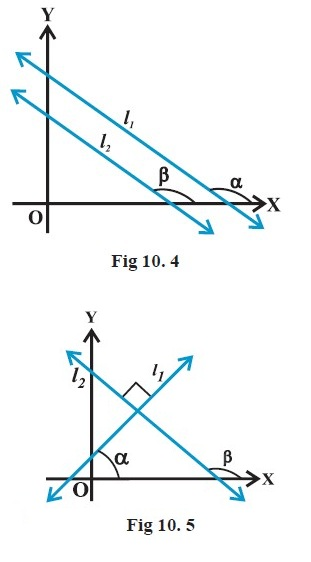
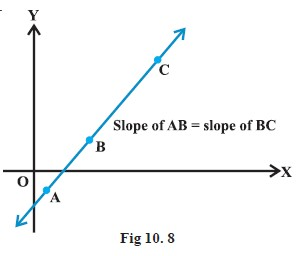
Introduction

`\color{green} ✍️` Let us have a brief recall of coordinate geometry done in earlier classes.
`\color{green} ✍️` To recapitulate, the location of the points `(6, – 4)` and `(3, 0)` in the `XY-`plane is shown in Fig 1.
We may note that the point `(6, – 4)` is at `6` units distance from the `y-`axis measured along the positive `x-`axis and at `4` units distance from the `x-`axis measured along the negative `y-`axis.
`\color{green} ✍️` Similarly, the point `(3, 0)` is at `3` units distance from the `y`-axis measured along the positive `x`-axis and has zero distance from the `x-` axis.
We also studied there following important formulae:
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` ` \ \ \ \ 1.` `color{green}("Distance between the points")` `P \ (x_1, y_1)` and `Q \ (x_2, y_2)` is
` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \color{blue}(PQ=sqrt((x_2-x_1)^2+(y_2-y_1)))`
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` ` \ \ \ \ \ 2.` The coordinates of a point dividing the line segment joining the points `(x_1, y_1)` and `(x_2, y_2)` internally, in the ratio `m: n` are `color{blue} ( (((mx_2+nx_1)/(m+n) , (my_2+ny_1)/(m+n)) )`
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` ` \ \ \ \ \ \ 3. ` In particular, if `m = n,` the coordinates of the mid-point of the line segment joining the points `(x_1, y_1)` and `(x_2, y_2)` are `color{blue} (((x_2+x_1)/2 , (y_2+y_1)/2))`
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` `\ \ \ \ \ \ \ 4. ` `color{green}("Area of the triangle")` whose vertices are `(x_1, y_1), (x_2, y_2)` and `(x_3, y_3)` is
`color{blue} (=1/2| x_1( y_2 − y_3) + x_2( y_3 − y_1) + x_3( y_1 − y_2)|) `
`"Remark "` If the area of the triangle `ABC` is zero, then three points `A, B` and `C` lie on a line, i.e., they are collinear.
`\color{green} ✍️` To recapitulate, the location of the points `(6, – 4)` and `(3, 0)` in the `XY-`plane is shown in Fig 1.
We may note that the point `(6, – 4)` is at `6` units distance from the `y-`axis measured along the positive `x-`axis and at `4` units distance from the `x-`axis measured along the negative `y-`axis.
`\color{green} ✍️` Similarly, the point `(3, 0)` is at `3` units distance from the `y`-axis measured along the positive `x`-axis and has zero distance from the `x-` axis.
We also studied there following important formulae:
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` ` \ \ \ \ 1.` `color{green}("Distance between the points")` `P \ (x_1, y_1)` and `Q \ (x_2, y_2)` is
` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \color{blue}(PQ=sqrt((x_2-x_1)^2+(y_2-y_1)))`
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` ` \ \ \ \ \ 2.` The coordinates of a point dividing the line segment joining the points `(x_1, y_1)` and `(x_2, y_2)` internally, in the ratio `m: n` are `color{blue} ( (((mx_2+nx_1)/(m+n) , (my_2+ny_1)/(m+n)) )`
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` ` \ \ \ \ \ \ 3. ` In particular, if `m = n,` the coordinates of the mid-point of the line segment joining the points `(x_1, y_1)` and `(x_2, y_2)` are `color{blue} (((x_2+x_1)/2 , (y_2+y_1)/2))`
`\color { maroon} ® \color{maroon} ul (" REMEMBER")` `\ \ \ \ \ \ \ 4. ` `color{green}("Area of the triangle")` whose vertices are `(x_1, y_1), (x_2, y_2)` and `(x_3, y_3)` is
`color{blue} (=1/2| x_1( y_2 − y_3) + x_2( y_3 − y_1) + x_3( y_1 − y_2)|) `
`"Remark "` If the area of the triangle `ABC` is zero, then three points `A, B` and `C` lie on a line, i.e., they are collinear.